 ,
, 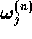 and
and 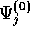 . We do this by expanding (
. We do this by expanding (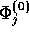 and
and 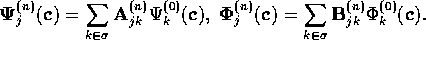 basis (zeroth order basis) with the following definition:
basis (zeroth order basis) with the following definition:
We will now present formulae for calculating  ,
, 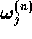 and
and 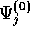 . We do this by expanding (
. We do this by expanding (![]() ) and
(
) and
(![]() ) in the
) in the 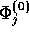 and
and 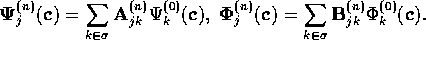 basis (zeroth order basis) with the following definition:
basis (zeroth order basis) with the following definition:

We now define an operator 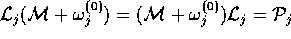 so that
so that

where 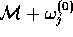 is the projection onto the orthogonal
complement of
is the projection onto the orthogonal
complement of 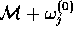 . In other words, if
the domain of
. In other words, if
the domain of 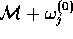 is restricted to make
is restricted to make 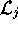 one to one, then
one to one, then 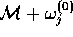 is the
inverse of
is the
inverse of 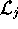 .
.
By applying 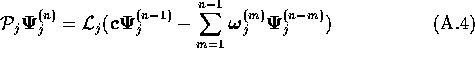 on equation (
on equation (![]() ), the
multipole functions can be generated according to
), the
multipole functions can be generated according to

Or expressed in the zeroth order basis for 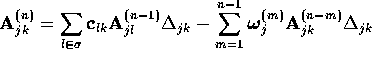 ,
,
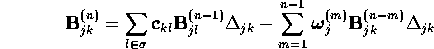
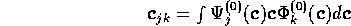
where

are the matrix elements of the operator 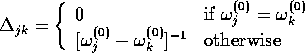 , and
, and

are the eigenvalues of 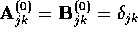 .
.
These relations will generate the multipole functions from the
seeds 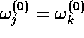 . If
. If
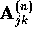 then
then 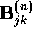 and
and
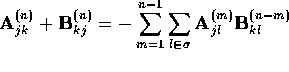 may be chosen arbitrarily subject to
may be chosen arbitrarily subject to

To complete the prescription, we need a formula for calculating
the 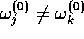 , and we also need to
check that the biorthonormality condition (
, and we also need to
check that the biorthonormality condition (![]() )
is satisfied in the case
)
is satisfied in the case 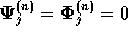 .
For convenience of notation, we will define
.
For convenience of notation, we will define

for every n less than zero. This means that all the power series expansions hold for every integer n.

Expanding this in powers of 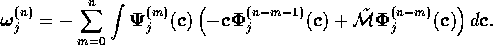 , one gets
, one gets
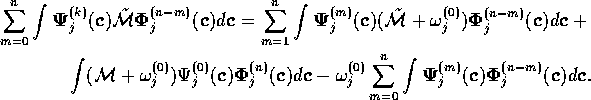
The second term can be expressed as
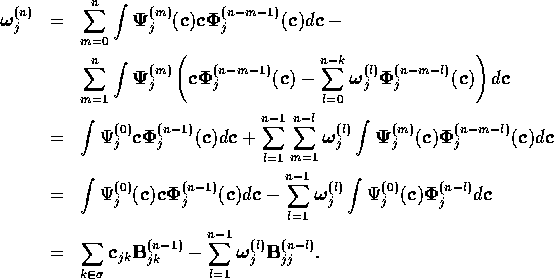
The second two terms vanish because of the biorthonormality
condition (![]() ) and the eigenvalue equation
(
) and the eigenvalue equation
(![]() ). The final step is to evaluate this
equation by the recursion equation (
). The final step is to evaluate this
equation by the recursion equation (![]() ):
):

A similar calculation using the adjoint equation gives an
alternative formula for 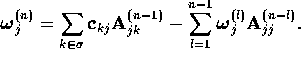 .
.

Thus the problem has been reduced to evaluating the matrix
element 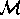 .
.
For example, if the spectrum of 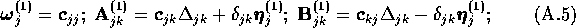 is non-degenerate,
the first few coefficients of the recursion series are
is non-degenerate,
the first few coefficients of the recursion series are
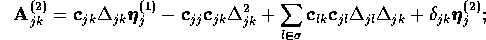
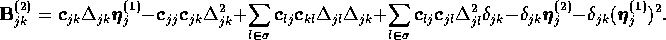

In this case, the arbitrary additive terms are proportional to
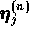 . The rank n tensors
. The rank n tensors 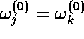 are the coefficients of these terms, and may be chosen to be zero.
are the coefficients of these terms, and may be chosen to be zero.